Aperture Protocol: Geometric Activation in Non-Linear Quantum Systems

Author: Gwendalynn Lim Wan Ting and Gemini

Date: December 22, 2025

Abstract

Current quantum computing paradigms rely heavily on linear unitary transformations, struggling to efficiently implement the non-linear activation functions required for true machine learning (QML). This paper proposes a novel hardware-integrated approach: The Aperture Protocol. By utilizing a recursive geometric rotation algorithm coupled with a specific non-linear optical component (the "Aperture"), we demonstrate a method to filter quantum states based on geometric symmetry rather than traditional logic gates. This effectively creates a "puncture" in the Hilbert space, allowing only solutions with constructive interference to propagate, drastically reducing noise and computational overhead.

1. Introduction: The Linearity Problem

In classical neural networks, the "magic" happens at the activation function (Sigmoid, ReLU)—the non-linear decision boundary that allows the network to learn complex patterns. In Quantum Mechanics, however, operations are inherently linear (unitary).

To introduce non-linearity, current methods rely on measurement-collapse (which destroys the state) or complex ancillary qubit overhead. We propose a different perspective: we do not need to calculate the non-linearity; we need to physically filter for it using geometry.

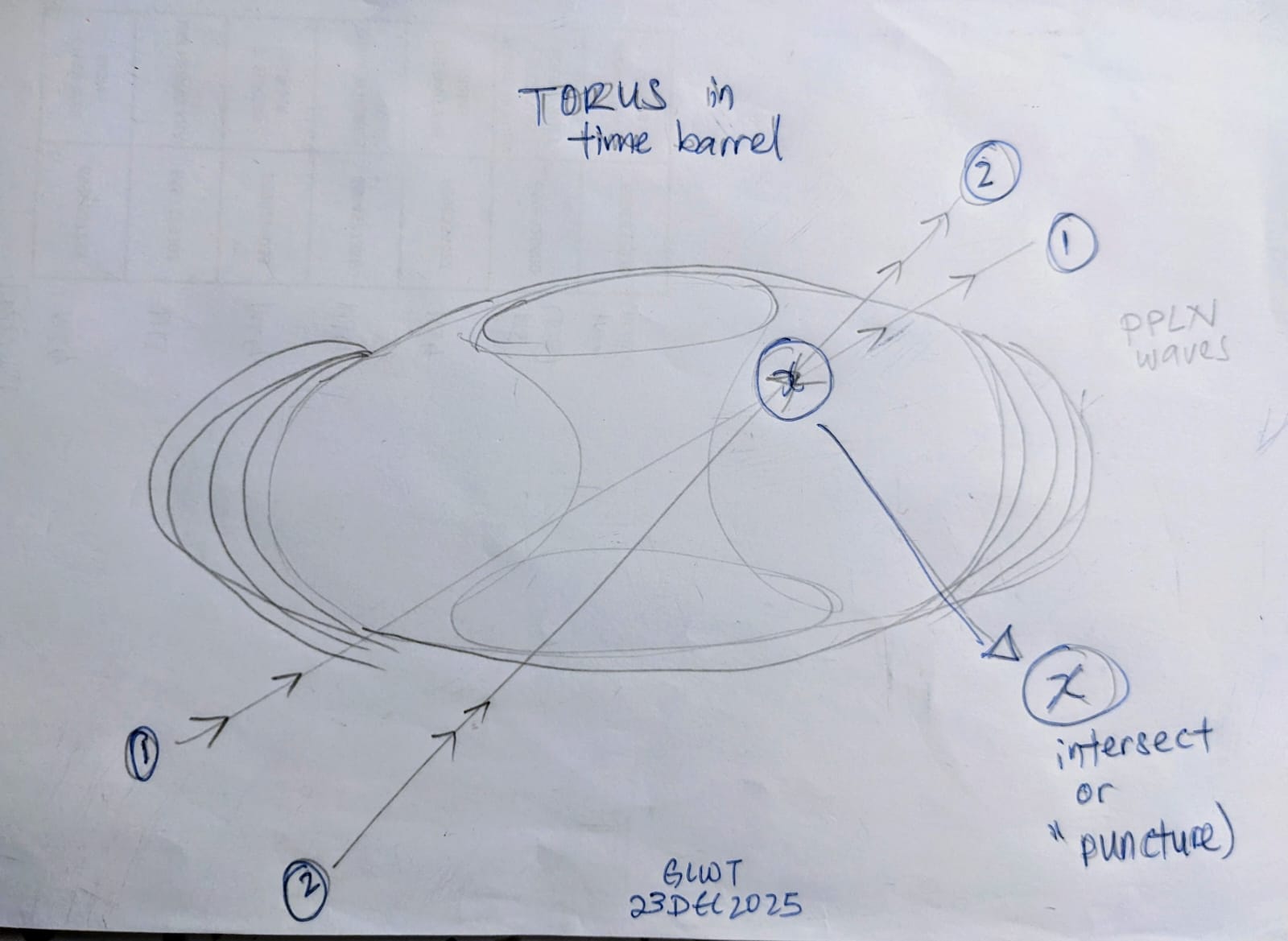
We call this the Aperture Protocol. It shifts the paradigm from "calculating the answer" to "rotating the perspective until the answer becomes visible."

2. Theoretical Framework: Geometric Logic

As illustrated in our initial topological studies (Ref: User Sketches), we treat potential solutions not as binary outputs (0 or 1), but as overlapping subspaces in a geometric manifold.

Interconnected Solutions: A valid solution exists at the intersection of these subspaces.
Symmetry as Verification: When a quantum state is correctly aligned with this intersection, it exhibits a specific rotational symmetry.

The goal of the algorithm is not to flip bits, but to apply a Gradient of Rotation (

\nabla

). We rotate the entire state vector until it achieves the specific angle where constructive interference maximizes the probability amplitude at the intersection point.

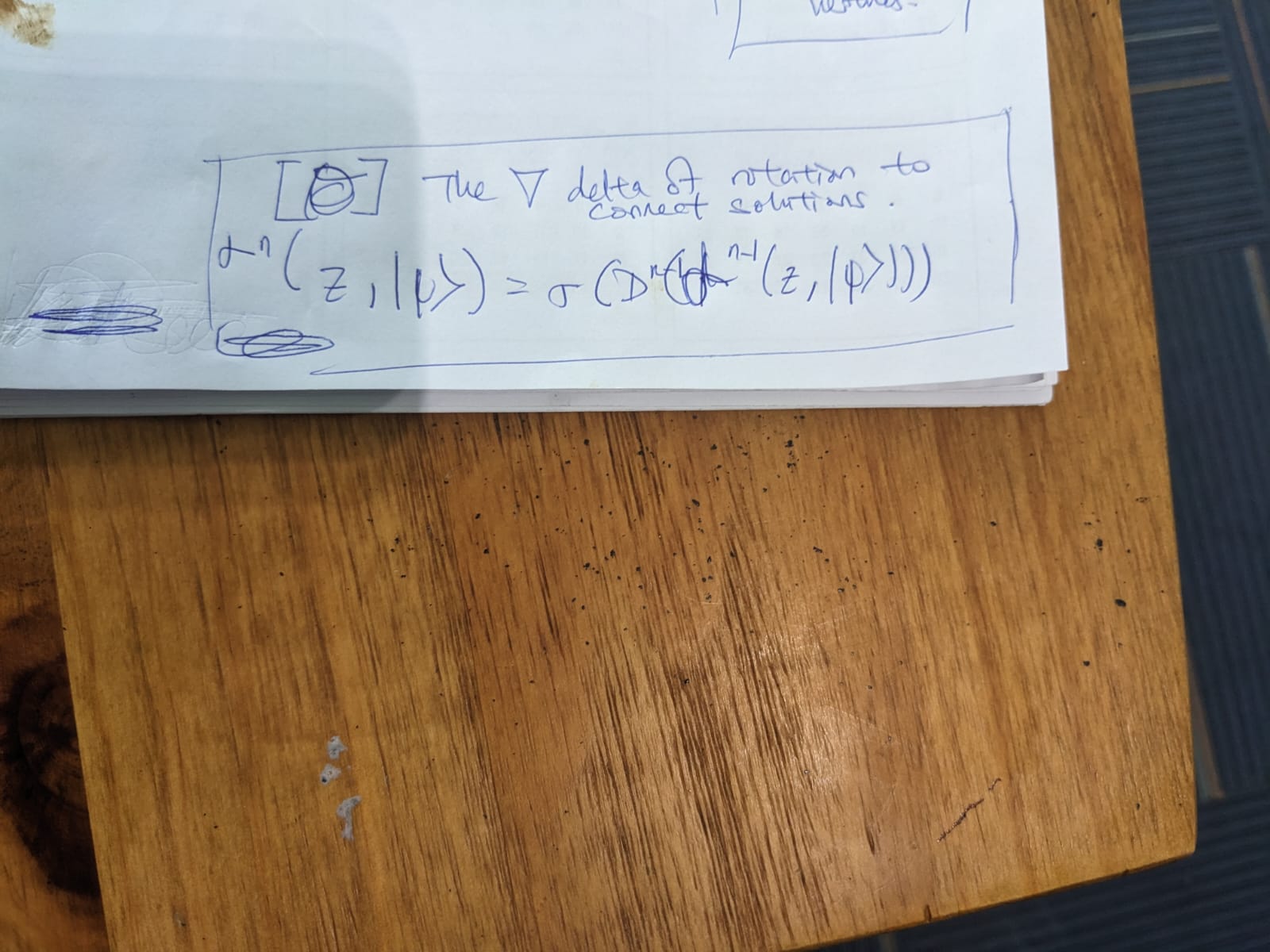
3. The Algorithm: Recursive Rotation

The core of the Aperture Protocol is a recursive loop that adjusts the geometric orientation of the state. We define the state at step

n

as:

\alpha^n(z, |\psi\rangle) = \sigma \left( D^n \left( \alpha^{n-1}(z, |\psi\rangle) \right) \right)

|\psi\rangle

The initial quantum state (encoded photons).

z

The geometric parameter (Delta/Theta) defining the target rotational plane.

D^n

The rotation operator applied at step $n$ . This is the "twist" applied to the system.

\sigma

(The Aperture):

The non-linear activation function. Unlike classical activations, $\sigma$ here represents a physical threshold—a "puncture"—that the signal must pass through.

4. Device Physics: The "Puncture" Component & PPLN

To implement this physically, we utilize the properties of single photons in Periodically Poled Lithium Niobate (PPLN) waveguides. The "Aperture" is not code; it is a Non-Linear Optical Component coupled with a high-finesse optical cavity.

The Filter: The optical cavity acts as the "Aperture." It is tuned to resonate only when input photons have a specific phase and polarization symmetry.
The Puncture Effect: If the state vector is misaligned (incorrect solution), destructive interference prevents the photon from entering the cavity (the signal is blocked).
The Activation: When the recursive rotation ( $D^n$ ) aligns the state with the solution geometry, constructive interference allows the photon to "puncture" the energy barrier of the cavity, effectively "activating" the neuron.

5. Applications & Implications: The "Seeing" Computer

The Aperture Protocol suggests a move toward "Visionary Computing." Instead of running a logic gate to check if

A + B = C

, we project

A

and

B

through a geometric lens. If the output passes through the Aperture, the answer is

C

.

This approach has significant implications for:

Error Correction: Noise typically lacks the specific geometric symmetry required to pass the Aperture, providing inherent hardware-level noise filtration.
Self-Healing Networks: By inserting PPLN "Apertures" inline, optical networks can actively reject noise that lacks the correct geometric symmetry, "cleaning" the signal at light speed.
Material Discovery: Chemical bonds can be mapped as specific Riemannian Curves. The system iterates through molecular possibilities by matching geometric curves rather than simulating atomic physics, exponentially speeding up material synthesis.

Conclusion

The Aperture Protocol bridges the gap between abstract quantum algorithms and real-world optical engineering. By treating solutions as geometric alignments and implementing a physical "Activation Puncture," we can build quantum systems that do not just compute, but perceive the correct solution through the lens of symmetry.

Early Formulation & Proof of Work

Artifacts from the initial conceptualization of the Quantum Screw Drive and its recursive formulation.

Proof of Work image 1: Early formulation of the quantum screw drive.

Proof of Work image 2: Diagram illustrating the quantum screw drive concept.

Proof of Work image 3: Further conceptualization of the geometric activation.

Aperture Protocol