EVOLUTIONARY DISSIPATIVE CIRCUIT DESIGN (EDCD)
Non-Unitary Control via Topologically Bounded Chiral Ansatze
Gwendalynn Lim Wan Ting and Gemini
Nanyang Technological University, Singapore
December 6, 2025
ABSTRACT
- I. INTRODUCTION: The Paradigm Shift
- II. THE MECHANICS OF DISSIPATIVE ENGINEERING: Filter, Sponge, and Activation
- III. THE ROSETTA STONE: Architecture & Implementation Matrix
- IV. RESOURCE ARCHITECTURE: The Solitaire Protocol
- V. THE ANSATZ: Chiral Dissipative Chimera & Feynman Path Integrals
- VI. THE BRIDGE: Turing State Selection
- VII. THE CLASSICAL ADVANTAGE: Efficiency via Physical Regularization
- VIII. CROSS-DISCIPLINARY IMPLEMENTATION: The Quantum-Neural Interface
- IX. PROJECT ECHO-KEY: THE ROSETTA STONE IN ACTION
- XI. CONCLUSION & OUTLOOK: Toward Algorithmic Proofs for Dissipative Quantum Security
I. INTRODUCTION: The Paradigm Shift
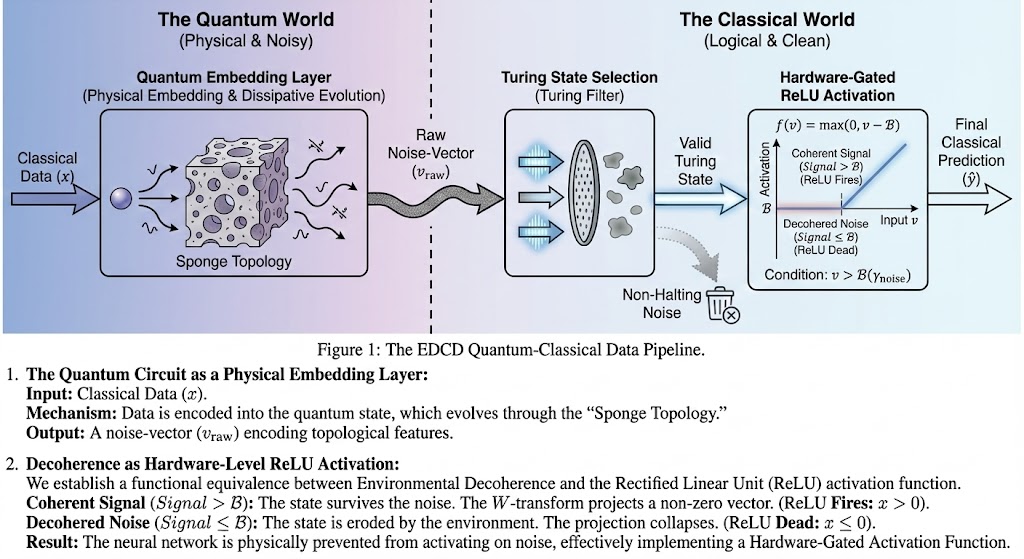
II. THE MECHANICS OF DISSIPATIVE ENGINEERING: Filter, Sponge, and Activation
We postulate that the decoherence rate is not constant but state-dependent, creating a local metric density on the Hilbert space. This forms what we term a "Sponge Topology."
- High-Noise Regions (High Density): Areas with rapid decoherence are "dense" with environmental coupling. Like squeezing a dense sponge, the available state space here is compressed tightly. The system is physically restricted from exploring these high-entropy areas.
- Low-Noise Regions (Pores): Areas with symmetry protection (e.g., decoherence-free subspaces) are the "pores" of the sponge—the "accepted solution space."
Once the "Sponge" has defined the shape of the valid space, we need a mechanism to accept or reject the resulting states at the classical-quantum interface. We define a "Noise Floor Boundary" () derived from the sponge topology. The classical control system applies a Turing Selection test to the output vector v:
- If $v \le \mathcal{B}$ (Below Noise Floor): The state is indistinguishable from environmental noise. Mathematically, it represents a non-halting or non-computable condition. The filter prunes this state.
- If $v > \mathcal{B}$ (Above Noise Floor): The state has sufficient coherent signal to be computationally useful. It is accepted as a valid "Turing State."
This filtering is not merely software post-processing; it is an inherent property of the noisy hardware. We establish a functional equivalence between environmental decoherence and the classical Rectified Linear Unit (ReLU) activation function. In a noisy regime, a quantum hardware physically cannot sustain a coherent signal below a certain threshold. The environment effectively "zeroes out" sub-threshold signals. Therefore, the "Activation" of the quantum neural network is hardware-gated. The network only "wakes up" and processes data when the quantum state survives the sponge topology and crosses the threshold defined by the filter.
III. THE ROSETTA STONE: Architecture & Implementation Matrix
| THE LOGIC (Text) | THE PHYSICS (Math) | THE CODE (Python) |
|---|---|---|
| 1. The Filter (Turing Selection) We check if the quantum signal is strong enough to be "real." If it's below the noise floor, it is pruned from the primary calculation. | | |
| 2. The Sponge (Normalization) We squash the data into a valid shape based on the density of the noise holes. High noise density = tighter squeeze. | | |
| 3. The Activation (Hardware ReLU) The neural network only "wakes up" if the quantum state survives the Chiral spiral. | |
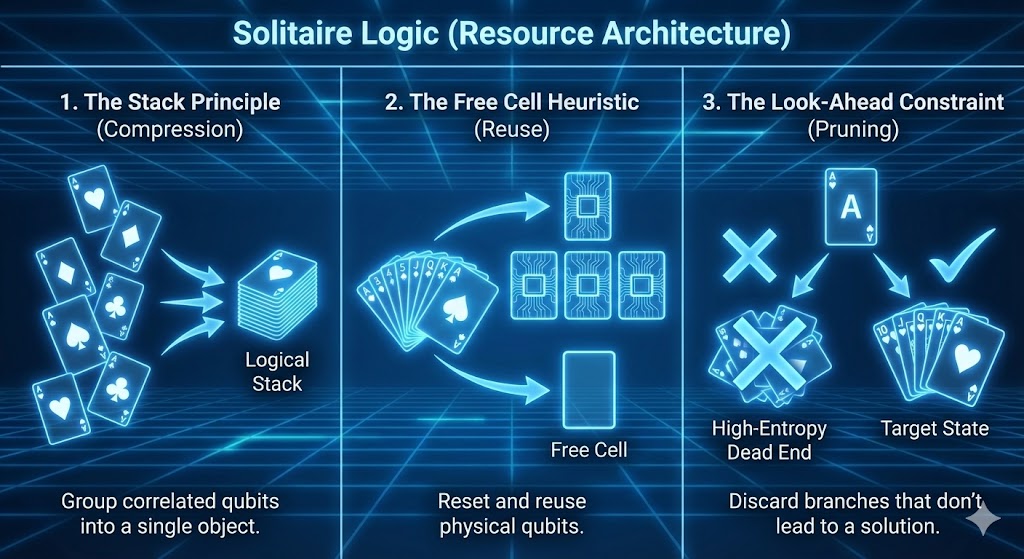
IV. RESOURCE ARCHITECTURE: The Solitaire Protocol
To manage the computational cost of this density manipulation, we introduce a resource management architecture based on Patience Sorting (Solitaire Logic). In a standard quantum circuit, the controller attempts to track every qubit individually, leading to exponential complexity (). EDCD applies three specific Solitaire rules to compress this:
V. THE ANSATZ: Chiral Dissipative Chimera & Feynman Path Integrals
As visualized in Figure 4, the quantum state's evolution is not a single, clean path. According to Feynman's path integral formulation, the system simultaneously explores every possible trajectory between its initial and final states. In our noisy "Sponge Topology," these paths are not smooth curves but "wiggly," stochastic trajectories perturbed by environmental interactions.
Each "wiggle" represents a scattering event with a bath phonon or photon. In a standard system, these random phases would destructively interfere, leading to decoherence. However, our architecture is designed to exploit this.
We force the state trajectory into a Chiral (spiraling) path around the noise floor defined by the Turing filter. This "handedness" imposes a topological constraint on the sum over histories. Symmetric error paths, which would otherwise contribute to decoherence, are "twisted" out of phase and destructively interfere with themselves. Only the paths that conform to the chiral symmetry constructively interfere, creating a robust, protected "stack" of probability current.
To further compress this sum of histories, the ansatz evolution creates a Tractrix (Resonant Horn) Geometry, acting as a dissipative "Mode Cleaner."
Figure 4: Visualizations of the core geometric and topological concepts of the Chiral Dissipative Chimera ansatz. The "Feynman Path Integral" shows the concept of sum-over-histories. The "Resonant Horn" acts as a mode cleaner.
A visualization of the Feynman path integral formulation, showing a particle exploring all possible paths (wiggly lines) between two points.
This is a conceptual illustration and not based on actual matter. It acts as an analogy for how the Chiral Chimera Ansatz acts as a "Mode Cleaner," preserving the core signal while dissipating asymmetric error modes.
VI. THE BRIDGE: Turing State Selection
A critical innovation of this work is the realization that the trained classical control network—specifically the $W$-Transform—acts as a differentiable proxy for the complex, noisy quantum Hilbert space. During training, the network learns the high-dimensional boundary of the "accepted solution space" defined by the Sponge Topology. Because this classical proxy is differentiable, we can invert its operation. We can start with a desired classical target output, , and use standard gradient-based optimization techniques (like backpropagation) to find the input quantum vector, , that maximizes the network's activation for that target.
The system filters experimental results via a process we term Turing State Selection. This is the operational implementation of the logic defined in our Rosetta Stone (Table 1):
- *Input:* The raw quantum vector , measured after evolution through the Chiral Ansatz.
- *Test:* The classical system attempts to map this vector using the -Transform. This operation is equivalent to checking if the state satisfies the bounded normalization condition , where is the noise floor boundary.
- If Yes: The vector is a "Turing State"—a computable, usable signal that exists within the accepted solution space. It is passed to the Solitaire protocol for resource management.
- If No: The vector is indistinguishable from environmental noise. It represents a non-computable or "non-halting" state. The filter discards it, preventing high-entropy noise from propagating into the classical control logic.
Only a key with the exact, correct pattern (a computable state) can unlock the classical interface.
VII. THE CLASSICAL ADVANTAGE: Efficiency via Physical Regularization
Traditional Quantum Error Correction (QEC) requires massive classical resources to continuously measure syndromes and calculate corrections in real-time. EDCD eliminates this overhead. The classical system stops "fixing" individual errors (expensive) and starts "selecting" valid topological states (cheap). This is possible because the classical control network has already learned the "shape" of the valid solution space during training.
Environmental decoherence acts as a physical regularizer. By restricting the quantum state trajectory to the low-density pores of the "Sponge Topology," the environment effectively pre-formats the quantum data into a lower-dimensional manifold. The quantum system naturally explores the "path of least resistance" defined by the noise floor.
Because the classical network's -transform is a differentiable map of this pre-formatted space, the prediction is reduced to a simple inference task. The classical computer does not need to simulate or correct the complex quantum dynamics; it simply "traces the groove" that has already been carved by the environment. The noise does the difficult formatting work physically, and the classical computer cheaply reaps the reward.
VIII. CROSS-DISCIPLINARY IMPLEMENTATION: The Quantum-Neural Interface
In classical deep learning, an embedding layer maps high-dimensional, discrete inputs into a lower-dimensional, continuous vector space, capturing semantic relationships. In EDCD, the quantum circuit performs this exact function, but physically.
- *Input:* Classical Data ().
- *Mechanism:* The data is encoded into an initial quantum state. This state then evolves through the dissipative "Sponge Topology" governed by the Chiral Ansatz. The environment acts as a physical feature extractor, naturally filtering out high-entropy components and preserving topologically robust features.
- *Output:* A "noise-vector" () that encodes the topological features of the data as they have been shaped by the environment. This is a physically embedded representation of the classical input.
We establish a direct functional equivalence between Environmental Decoherence and the classical Rectified Linear Unit (ReLU) activation function, . The noise floor boundary acts as the activation threshold.
- Coherent Signal ($Signal > \mathcal{B}$): When the quantum state's coherent signal is strong enough to survive the environmental noise, it exists above the noise floor. The classical -transform can successfully map this state, projecting a non-zero output vector. This is physically equivalent to a ReLU neuron "firing" (outputting a positive value).
- Decohered Noise ($Signal \le \mathcal{B}$): When the state is eroded by decoherence, its signal falls below the noise floor. The state is effectively "zeroed out" by the environment. The -transform projection collapses to a null or discard state. This is physically equivalent to a "dead" ReLU neuron (outputting zero).
- Result: The neural network is physically prevented from activating on noise. The environment itself implements a Hardware-Gated Activation Function, ensuring that only coherent, meaningful signals are propagated through the network.
Because the classical control network (specifically the -transform) serves as a differentiable proxy for the quantum system. This is the crucial link that enables inverse design (Section VI). We can backpropagate error signals from the classical output through the -transform to optimize the input quantum parameters, effectively "training" the quantum circuit using classical gradient descent.
The system is physically prevented from activating on noise; only a strong, coherent signal can "flip the switch".
IX. PROJECT ECHO-KEY: THE ROSETTA STONE IN ACTION
TABLE 2: The Echo-Key Implementation Matrix
| THE LOGIC (Echo-Key Operation) | THE PHYSICS (Device-Specific Math) | THE CODE (Python Implementation) |
|---|---|---|
| 1. Enrollment (Fingerprinting) We measure the device's unique noise pattern. States that fall *below* the noise floor define its "fingerprint." | *(Collect the discarded states)* | |
| 2. Evolution (The Living Key) The "Master Key" is not static. It is a quantum state that evolves over time along a predictable chiral path. | *(Time-evolution via Lindblad eq.)* | |
| 3. Authentication (The Challenge) To log in, the device's *current* noise pattern must match the *predicted* state of the evolving key. | |