Topological Peristalsis: Riemannian Geodesic Flows as a High-Efficiency Bridge for Hybrid Quantum-Classical State Selection

Author: Gwendalynn Lim Wan Ting, Independent Researcher & Incoming AI/ML Scholar (NTU)

Date: December 21, 2025

1. Executive Summary: The Geometric Solution

The central thesis of Project Capstone is a paradigm shift from linear calculation to geometric perception. Instead of attempting to overpower environmental "noise" with error correction, we propose a system that uses the inherent geometry of the problem to filter it out. The core innovation is the "Aperture"—a physical or algorithmic protocol that creates a "puncture" in the high-dimensional problem space. This Aperture is tuned to the specific geometric symmetry of a correct solution. Only states that exhibit this target symmetry can "pass through" the puncture, while incoherent noise, lacking the required geometry, is naturally filtered. This approach effectively weaponizes the environment, turning chaos into a resource for computation.

Visualizing the Core Concepts

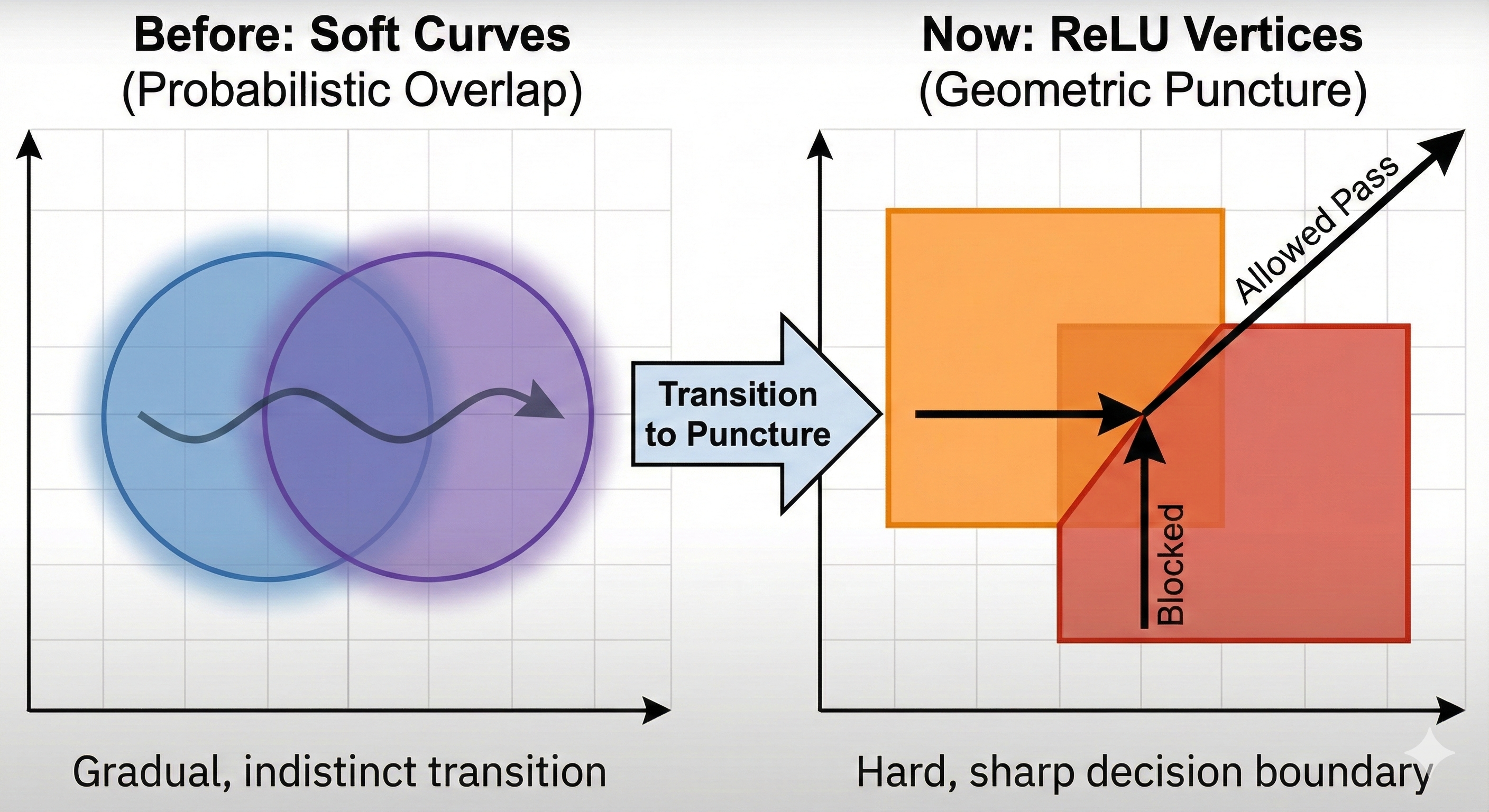
Visualizing the geometric "Puncture." The sharp angle of the ReLU function within the intersection visualizes a hard decision boundary imposed by geometry.

1. Visualizing the "Puncture"

The sharp angle of the ReLU function within the intersection is the literal "Puncture." It visualizes a hard decision boundary imposed by geometry. It shows that the signal doesn't just "slide" into the solution; it hits a distinct geometric wall where it is either blocked or allowed to pass.

Visualizing the Physics of the Vertex. This image shows that activation is a geometric inevitability. The 'flat line' is destructive interference when geometry is misaligned.

2. The Physics of the Vertex

This activation isn't software; it's a geometric inevitability. The 'flat line' represents the system when geometry is misaligned (destructive interference). The 'vertex' is the exact moment the operators align the state with the crystal's geometry, and the 'slope' is the sudden, constructive turn-on of the signal.

The Riemannian "Hunt" visualization. The system "flows" along the complex, curvy manifold, hunting for the solution.

3. The Riemannian "Hunt"

The system "flows" along the complex, curvy manifold, hunting for the solution. It doesn't know where the answer is; it's just following the curvature. When it hits that sharp geometric vertex—the intersection point—the curvature forces the state into the "Aperture," triggering the activation.

2. Mathematical Formulation: The Theta and Delta Operators

The engine of this framework is the Quantum Screw Drive governed by a recursive formula that manages the "Slinky" dynamics of the wave function:

The state at step $n$ is defined as:
$\alpha^n(z, |\psi\rangle) = \sigma(D^n(\alpha^{n-1}(z, |\psi\rangle)))$
$\alpha^n$ : The state at the current step.
$D^n$ : The rotation/transformation (The "Delta" or "Theta" shift).
$\sigma$ : The "Puncture" (The non-linear activation that filters the result).

This is driven by the interaction between the rotational phase and the transactional ripple:

The $\theta$ (Theta) Phase: Defines the circular orientation of the state vector, generating the Berry Phase (Geometric Memory) that allows the system to remember its state without physical contact.
The $\Delta$ (Delta) Ripple: The "Derivative of Rotation" ( $D^n$ ) that calculates the pitch required to "squeeze" data packets forward along the manifold.
The Result: Because Rotation = Translation, data (the "Milia Bundle") is carried passively by the geometry, eliminating the heat loss and friction of traditional "push" logic.

3. The Mechanism (The 'How')

The Aperture Protocol isn't just code; it describes a non-linear optical component and a specific sequence of physical actions.

The Input

Entangled photons (qubits) generated via SPDC (Spontaneous Parametric Down-Conversion) in a PPLN waveguide.

The Action

We don't flip bits; we rotate the state vector ( $z, \theta$ ) recursively.

The Logic

We look for the 'overlap' of subspaces (your intersecting circles).

The Trigger

When the rotation aligns with the solution's geometry, the system achieves symmetry, allowing the signal to pass through the 'Puncture' ( $\sigma$ ).

4. The Hardware: PPLN as a Geometric Learning Engine

We often think of algorithms as code, but in the Aperture Protocol, the algorithm is physical. The Periodically Poled Lithium Niobate (PPLN) waveguide is not just a passive pipe; it is the Geometric Quantum Learning Algorithm frozen in crystal. This hardware focus is critical because it eliminates the latency of converting a quantum result into a classical signal for processing—the 'learning' happens at the moment of interaction. The photon doesn't wait for a CPU to tell it if it's right; the geometry of the crystal itself acts as the judge, jury, and executioner of the signal.

Conclusion: A Unified Framework for Geometric Intelligence

Project Capstone is the culmination of our research, unifying the principles developed across our initiatives into a single, cohesive framework for building vector models of photonic and systemic systems. It demonstrates that the same geometric principles apply at every scale, from quantum hardware to global supply chains.

From Genesis: We take the core mathematical language of Riemannian Intelligence. The concept of a stable Base Manifold and a dynamic Tangent Corpus provides the architectural blueprint for a system that can learn without forgetting.
From Echo: We derive the hardware-level proof with Evolutionary Dissipative Circuit Design (EDCD). By treating a device's unique noise profile as a 'decoherence mold,' EDCD proves that geometric filtering can be physically instantiated, turning environmental noise into a computable, verifiable asset.
From Carbonite: We apply these principles at the macro scale. The Factor Beta (β) is a real-world, systems-level application of a directional derivative. It measures the 'curvature' of a complex entity (like a supplier) relative to the market, quantifying its geometric risk.

Together, these projects form a complete stack—from abstract mathematical theory to physical hardware and finally to global-scale application. Capstone proves that by focusing on the underlying geometry of a problem, we can create systems that are more efficient, stable, and intelligent by design.

5. Topological Encapsulation: A Geometric Defense for Digital Identity

Current digital identity is fragile because it is composed of discrete, independent data points. Our model renders it robust by making it Topologically Interlocked.

Geometric Encapsulation: An identity is not a collection of fields, but a cluster of quantized data packets (solitons) contained within a unified geometric envelope. This topological boundary protects the integrity of the core identity from external perturbation.
Topological Resilience: We utilize a structure analogous to a Hopf Fibration, where every constituent data packet is geometrically linked to every other. An attack on a single data point would require distorting the entire topological structure, making localized fraud geometrically infeasible.
Dynamic Equilibrium: Instead of being static, solutions exist in a state of dynamic equilibrium. They are immediately available when queried but remain fluid and non-static, preventing the vulnerabilities associated with fixed, predictable targets.

6. Global Hilbert Space: Financial Market Optimization

By treating the Stock Market as a single, massive Hilbert Space, we move from "prediction" to "topological navigation".

Market Geodesics: Wealth trajectories follow the path of least resistance (Geodesics), ensuring efficiency regardless of specific market points.
The Journey Invariant: If a participant understands the "Curve" of their journey, their target efficiency remains constant, effectively insulating them from systemic collapse.

A hero image for Project Capstone, representing light, optics, and geometric filtering.

The Aperture Protocol

A detailed look into the original manuscript, which establishes the physical implementation of these principles through a hardware-integrated geometric filter.

This protocol details the 'Aperture'—a non-linear optical component that creates a 'puncture' in Hilbert space, allowing only solutions with specific rotational symmetries to propagate. It serves as the physical manifestation of the high-level principles discussed in the main paper.

Read the Aperture Protocol